Раскраска графа
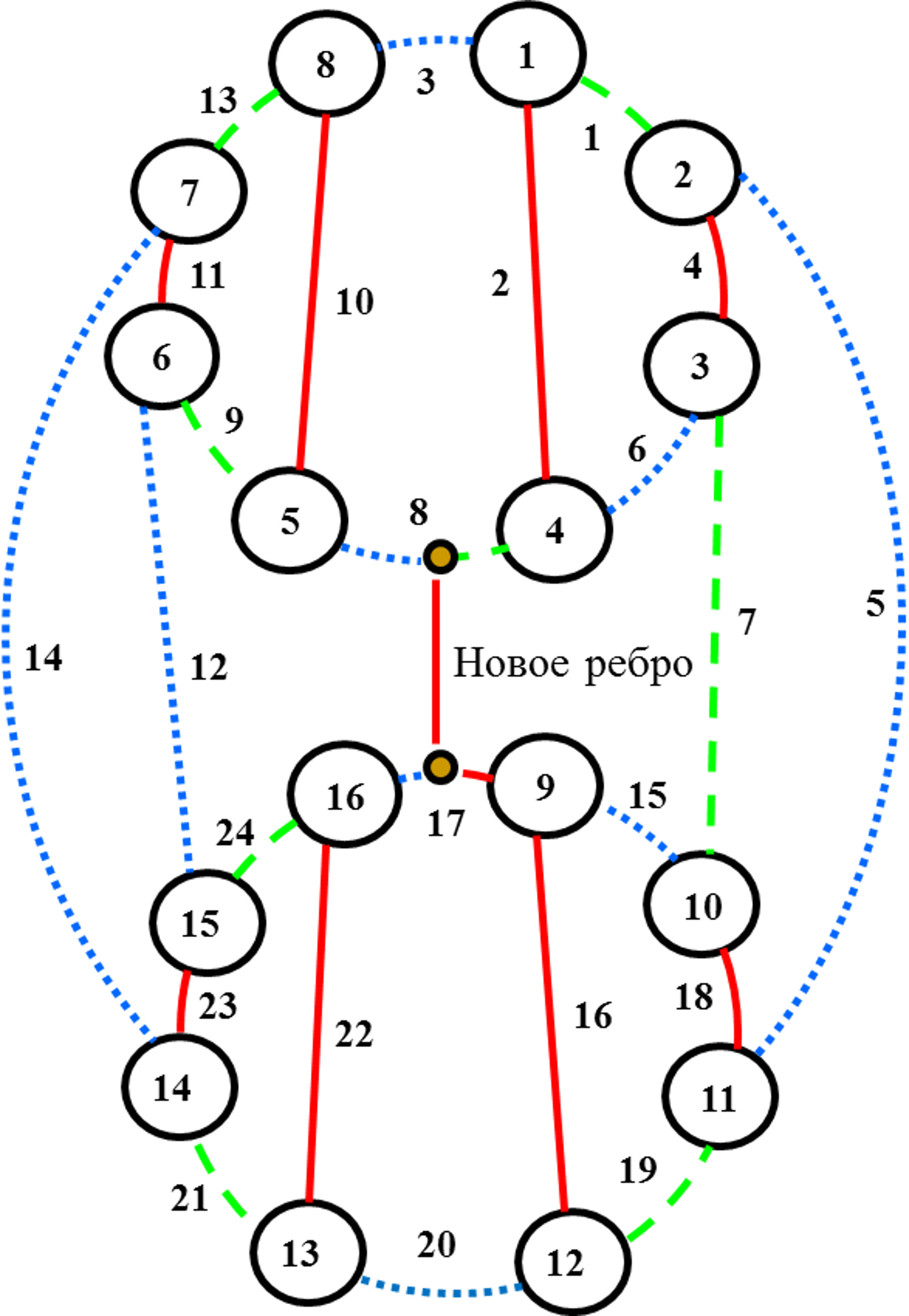
В этой записи я решил представить алгоритм, придуманный мной под впечатлением от распределённых distributed алгоритмов. Алгоритм строит субоптимальную правильную вершинную раскраску неориентированного графа. Алгоритм довольно прост и, возможно, был в том или ином виде представлен в литературе. Под конфликтами понимается наличие одинаково окрашенных вершин-соседей. Если вершину v перекрасить в цвет c , то конфликт будет разрешён при условии сохранения прежних цветов соседями v.
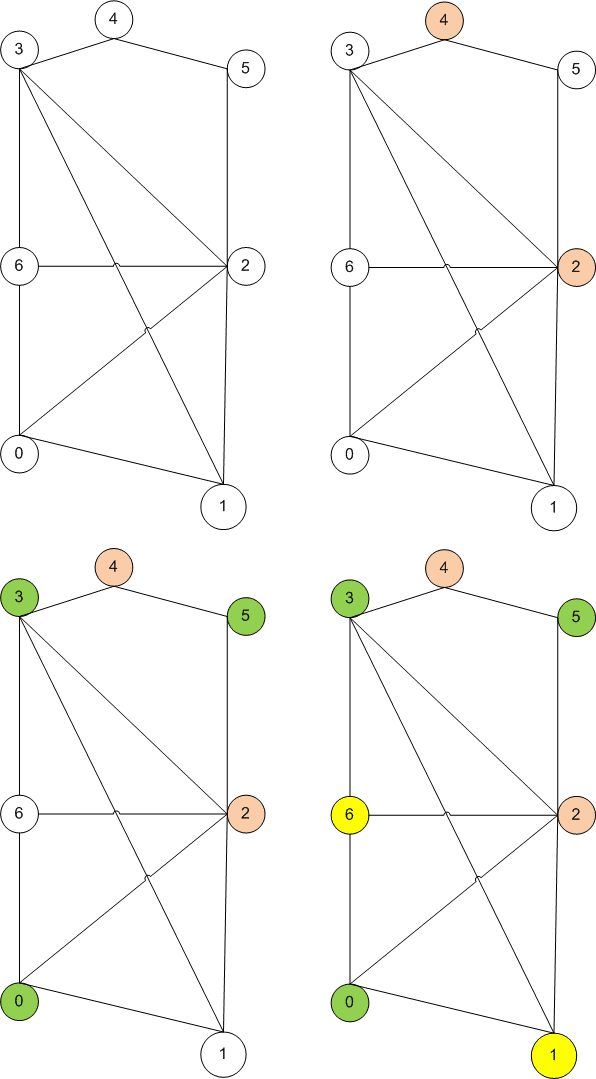
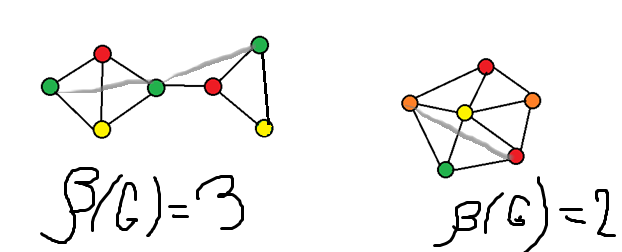


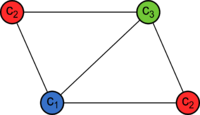
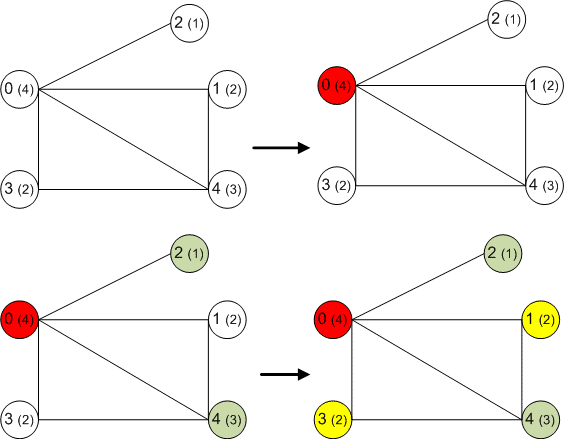
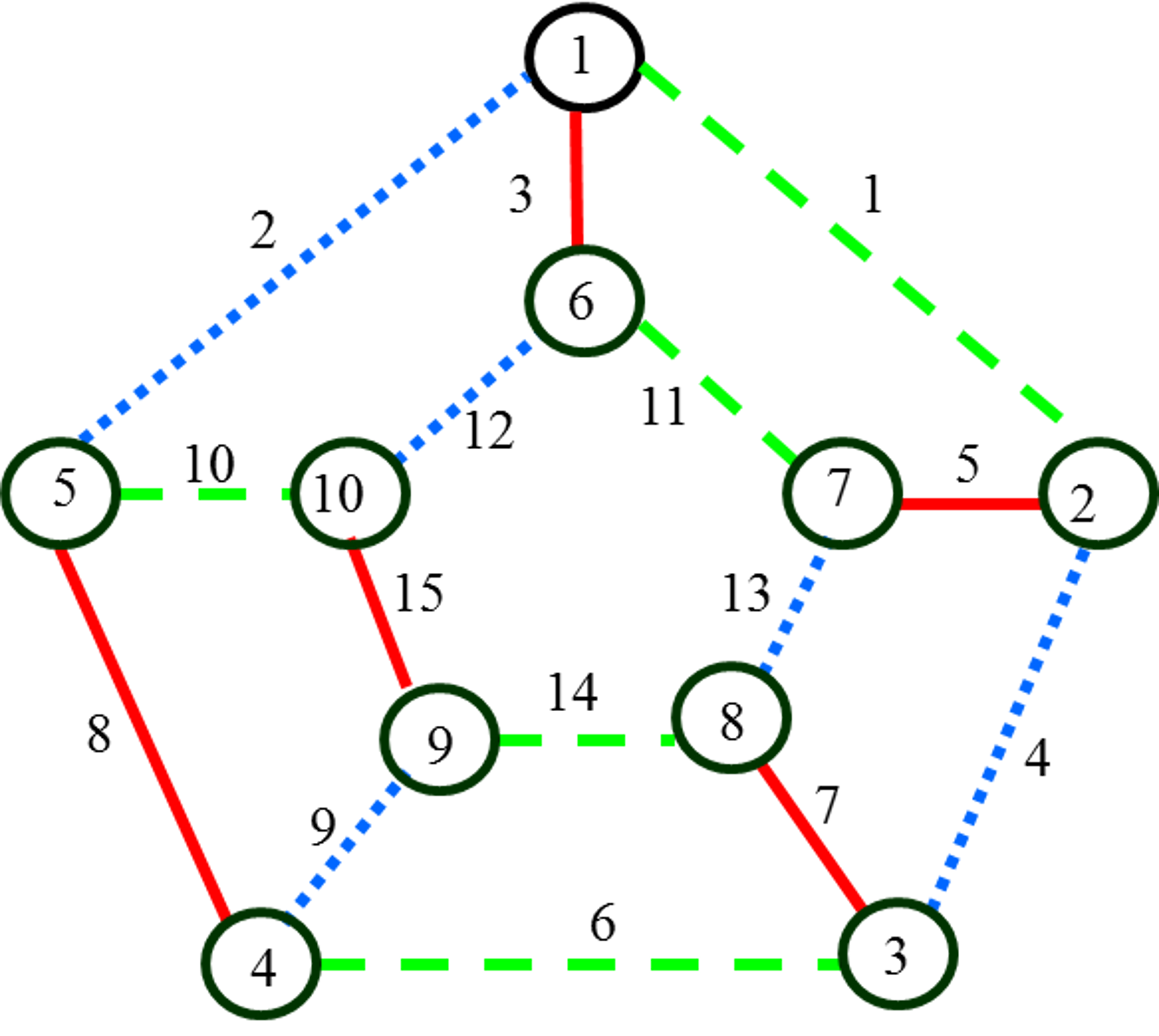



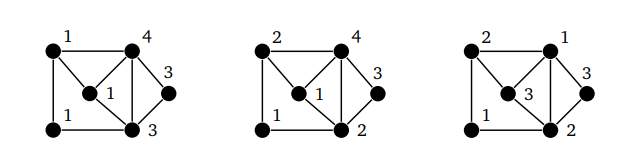
В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах. Также покажем примеры раскраски графов разных типов, так как в каждом случае этот процесс немного отличается. Цвета — это целые положительные цифры. Графы нужно раскрашивать так, чтобы соседние вершины имели разные цвета. Еще стоит использовать как можно меньше цветов.
- Публикации
- Раскраска представляет собой маркирование вершин графа таким образом, чтобы у смежных вершин маркеры не совпадали.
- Раскраской вершин графа называется назначение цветов его вершинам.
- Теорема о четырех цветах — это математический вопрос, который возник еще в 19 веке. Он заключается в том, можно ли раскрасить любую карту, используя только четыре цвета, таким образом, чтобы ни одна из двух соседних областей не имела одинакового цвета.
- Алгоритм раскраски графа
- Раскраска графа это такая разметка графа, при которой любым двум смежным вершинам соответствуют разные цвета.
- Download now.
- Корректной раскраской графа в два цвета называется такая раскраска, что никакое ребро не соединяет две вершины одного цвета.



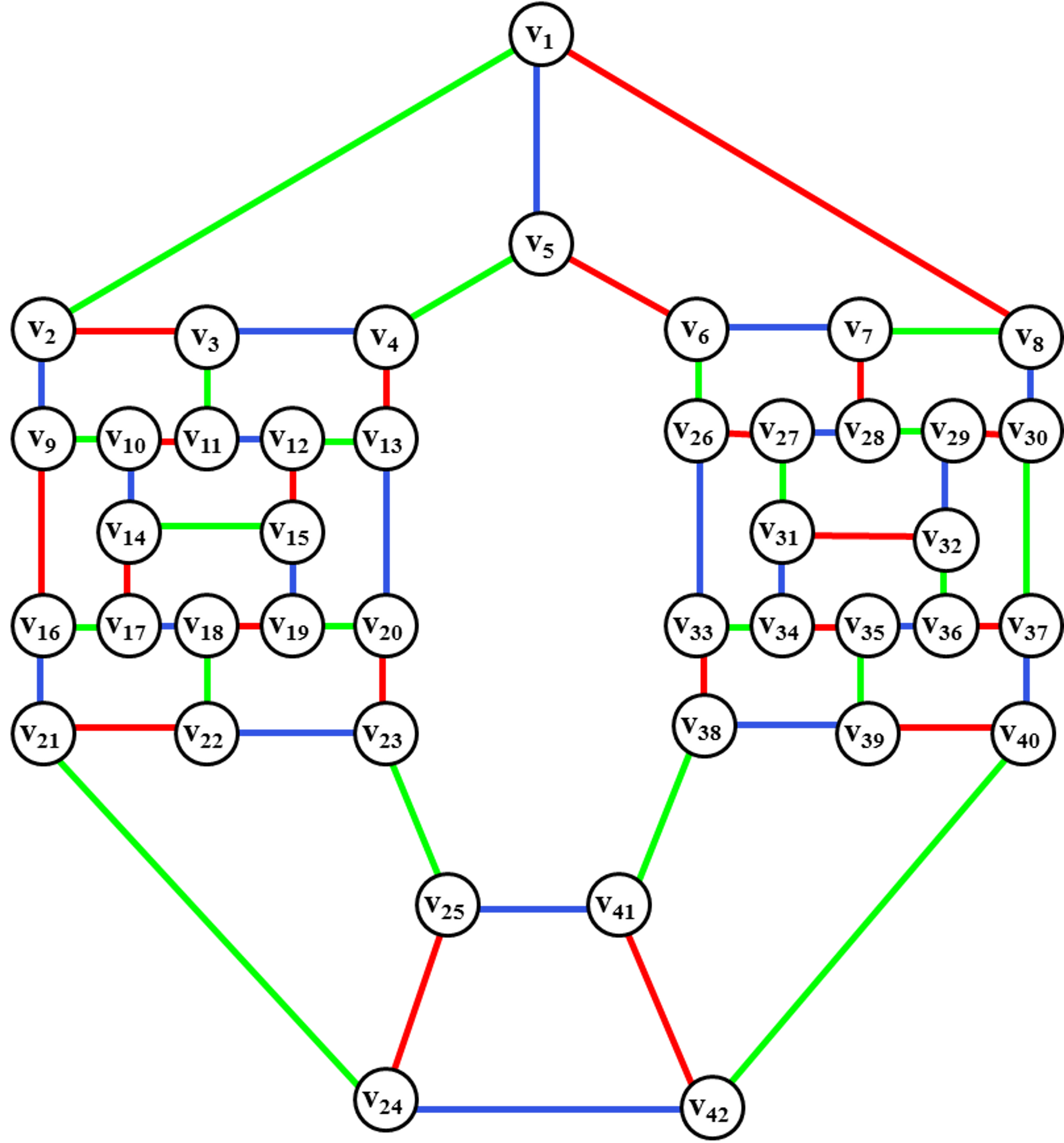




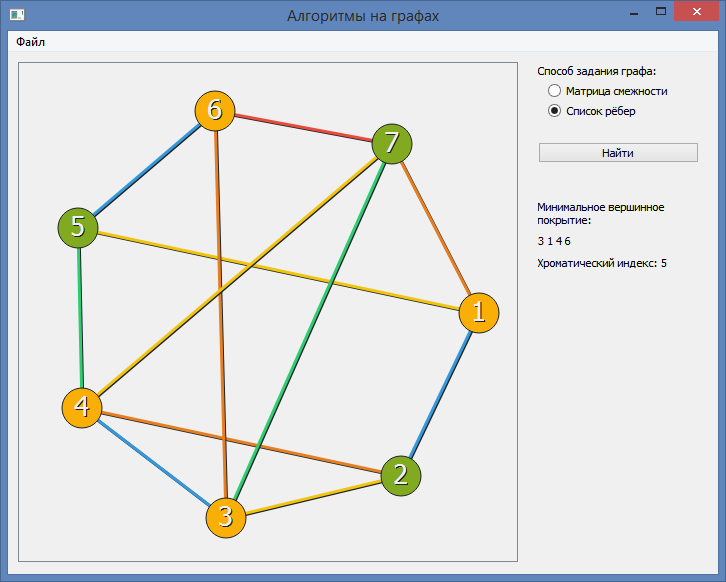
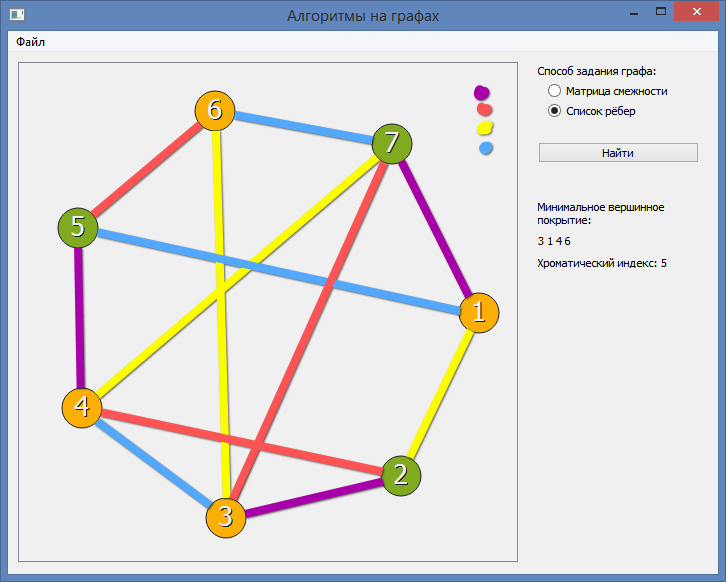
Алгоритм раскраски графа позволяет находить точное или приближенное значение хроматического числа произвольного графа и соответствующую этому значению раскраску вершин. Граф G называют r-хроматическим, если его вершины могут быть раскрашены с использованием r цветов красок так, что не найдется двух смежных вершин одного цвета. Наименьшее число r, такое, что граф G является r-хроматическим, называется хроматическим числом графа G.